

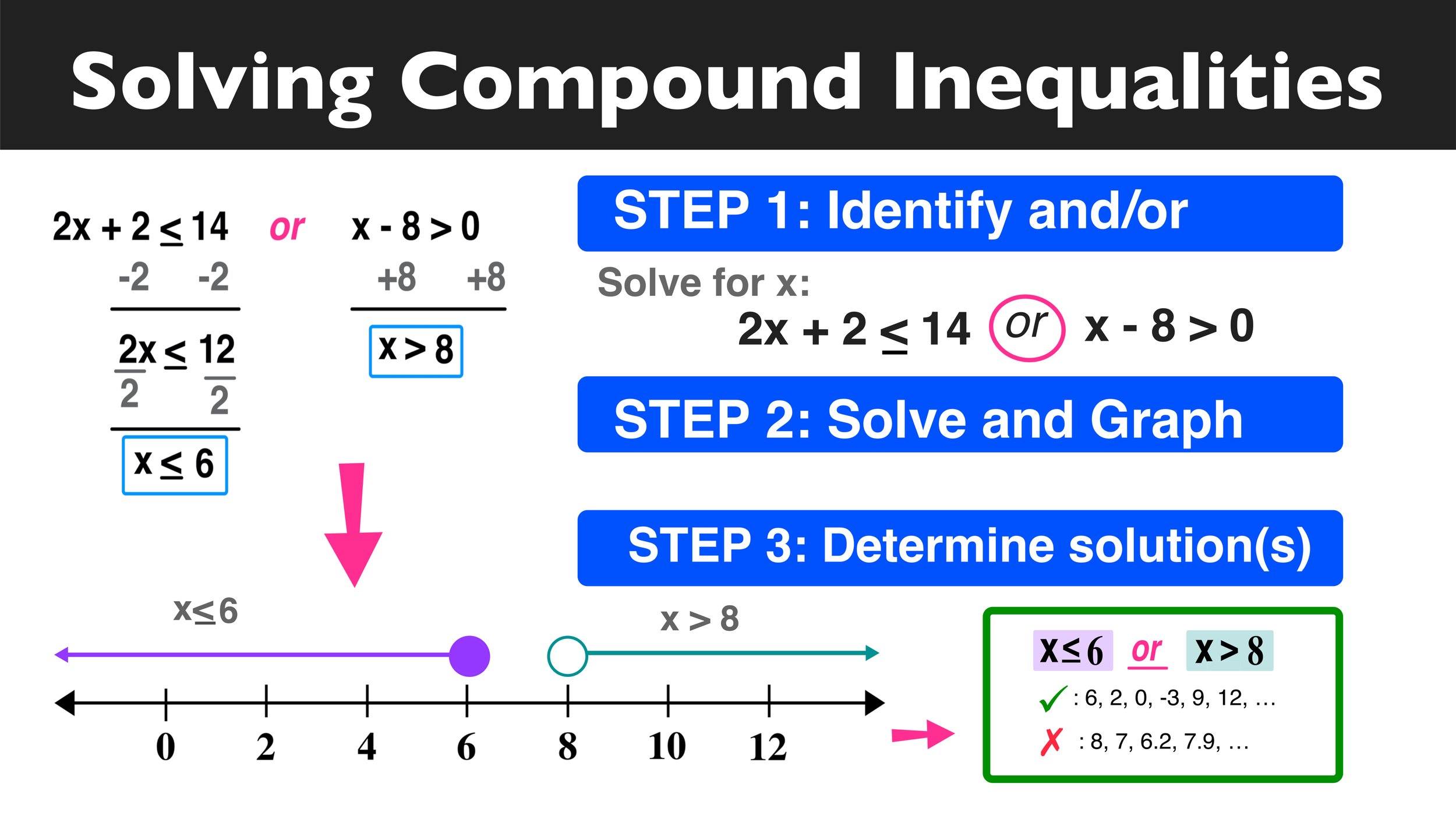
Being able to create, analyze, and solve a compound inequality using a compound inequality graph is an extremely important and helpful math skill that can be applied to many math concepts commonly found in pre-algebra, Algebra I, Algebra II, and even Pre-Calculus and Calculus. While many students may be intimidated by the concept of a compound inequality when they see unusual looking graphs containing circles and arrows, but working with compound inequalities is actually quite simple and straightforward.
The following free How to Solve Compound Inequalities step-by-step lesson guide will teach you how to create, analyze, and understand compound inequalities using an easy and effective three-step method that can be applied to any math problem involving a compound inequality or a compound inequality graph. As a student, if you can follow the three steps described in this lesson guide, you will be able to easily and correctly solve math problems involving compound inequalities.
Are you ready to get started? Before you learn about creating and reading compound inequalities, let’s review a few important vocabulary words and definitions related to inequalities.
Before we explore compound inequalities, we need to recap the exact definition of an inequality how they compare to equations.
What is an equation?
Definition: In math, an equation is a statement that shows that two mathematical expressions are equal to each other using an “=” sign.
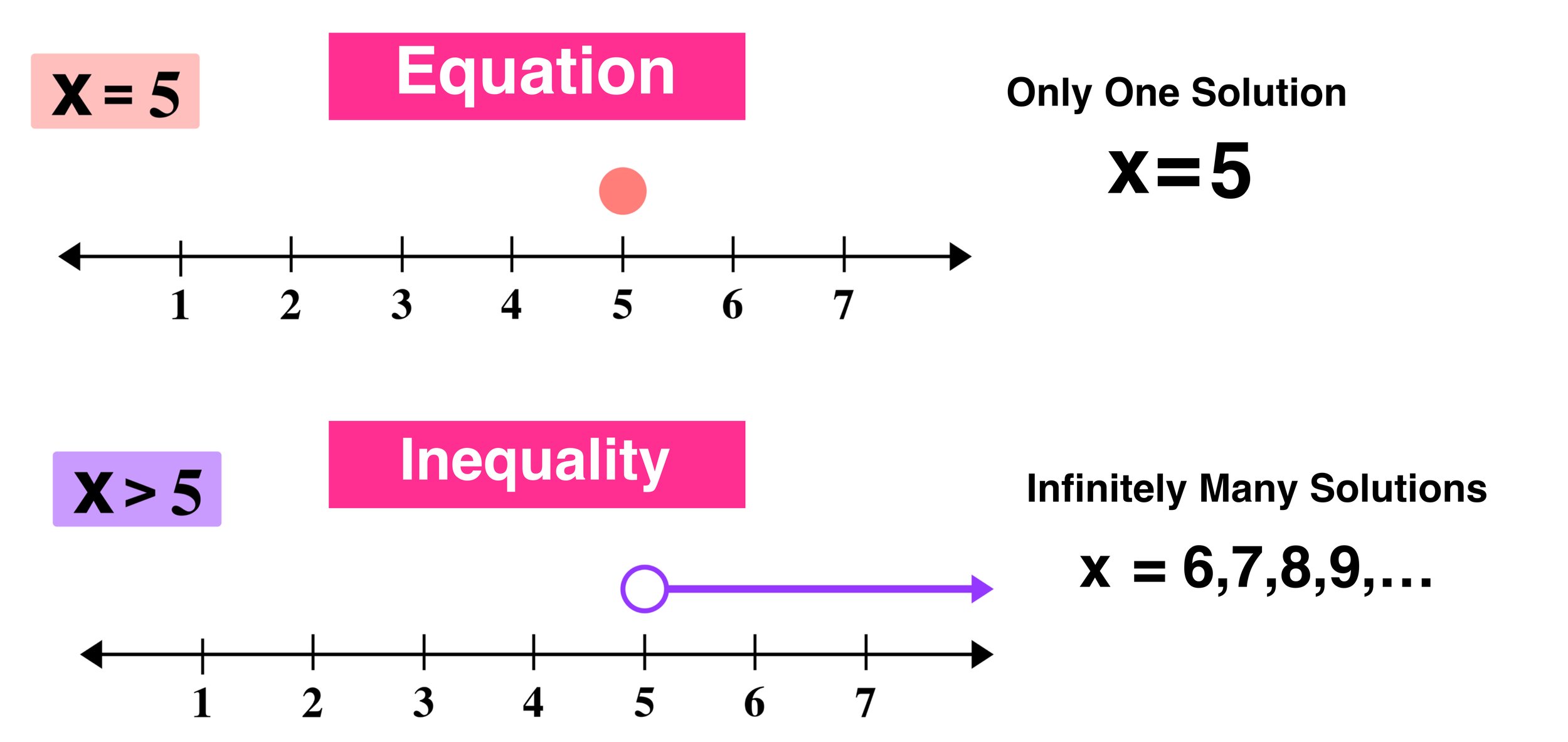
For example, x=5 is an equation where the variable and x are equal to a value of 5 (and no other value).

It is important to note that equations are limited to only one possible solution, so, in this case, 5 is the only possible value that x can be equal to, and any other value would not apply.
The only solution: 5
What is an inequality?
Definition: In math, an inequality is a relationship between two expressions or values makes a non-equal comparison.
For example, x>5 is an inequality that means “x is greater than 5,” where, unlike an equation that has only one solution, x can have infinitely many solutions, namely any value that is greater than 5.
We can visualize the simple inequality x>5 on the number line below as follows:

In comparison to equations, inequalities are not limited to only one possible solution. In fact, inequalities have infinitely many solutions.
In this case, solutions to the inequality x>5 are any value that is greater than five (not including five).
Examples of solutions: 6, 7, 10, 105, 2,500 (all of these values satisfy the inequality because they are greater than 5)
Examples of non-solutions: 5, 4, 0, -17, -1,001 (none of these values satisfy the inequality because they are not greater than 5)
Before we move onto exploring inequalities and compound inequalities, it’s important that you understand the key difference between an equation and an inequality.
In essence, the key difference is between an equation and an inequality is:
Now that you understand the difference between and equation and an inequality, you are ready to learn how solve compound inequalities and read compound inequality graphs.
But first, let’s quickly recap how to graph simple inequalities on the number line.
There are four types of inequality symbols:
It is important to understand the differences between these symbols, namely the significance of the line underneath a greater than or less than symbol and how it relates to the solution of an inequality and its graph on the number line.
For example, consider the following inequalities: x < 9 and x ≤ 9
The second inequality x ≤ 9, has a solution of any value that is less than 9 AND the value 9 itself (since 9 is greater than or equal to 9).
On the number line, the difference between these two types of inequalities is denoted by using an open or closed (filled-in circle). The open circle means that the corresponding value is not included in the solution set, while the closed circle means that the corresponding value is included in the solution set.